Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 8.8

8.8) Um rojão, lançado segundo um ângulo de 45°, explode em dois fragmentos ao atingir sua altura máxima, de $25m$; os fragmentos são lançados horizontalmente. Um deles, de massa igual a $100g$, cai no mesmo plano vertical da trajetória inicial, a $90m$ de distância do ponto de lançamento. O outro fragmento tem massa igual a $50g$. (a) A que distância do ponto de lançamento cai o fragmento mais leve? (b) Quais são as velocidades comunicadas aos dois fragmentos em consequência da explosão? (c) Qual é a energia mecânica liberada pela explosão?

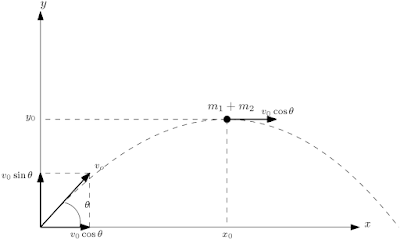
a) Adotando o referencial no ponto de lançamento, com eixo $ox$ va horizontal,

Antes de explodir o rojão de massa $m_1+m_2$ tem apenas energia cinética na horizontal e apenas potencial na vertical, tal energia potencial $E_p=mgy_0$, porém, depois do lançamento era energia cinética dada pela componente em $y$ da velocidade inicial $v_0$ que foi totalmente convertida em energia potencial $E_p$, logo usando conservação de energia encontramos a velocidade inicial $v_0$,

$$\frac{1}{2}(m_1+m_2)v_0^2\sin^2\theta=(m_1+m_2)gy_0$$

Explicitando $v_0$ obtemos,

$$v_0=\frac{\sqrt{2gy_0}}{\sin\theta}\ \ \ (1)$$

O movimento do rojão até o máximo da trajetória parabólica é descrita pela equação,

$$\left\lbrace \begin{array}{ll}
x=v_0\cos\theta t\\
y=v_0\sin\theta t -\frac{1}{2}gt^2\\
\end{array}\right. $$

Usando o resultado (1) as equações da posição são,


$$\left\lbrace \begin{array}{ll}
x=\sqrt{2gy_0}\cot\theta t\ \ \ (2)\\
y=\sqrt{2gy_0}t -\frac{1}{2}gt^2\ \ \ (3)\\
\end{array}\right. $$

Derivando a equação (3) obtemos a velocidade em y que no ponto máximo deve ser nula, com tal equação, podemos encontrar o tempo de subida $t_s$

$$v_y=\sqrt{2gy_0} -gt_s=0\Rightarrow$$

$$t_s=\frac{\sqrt{2gy_0}}{g}$$

Com o tempo de subida podemos encontrar a posição $x_0$ do máximo do movimento parabólico aplicando $t_s$ em (2),

$$x_0=2y_0\cot\theta\ \ \ \ (4)$$

Logo após a explosão o pedaço de maior massa $m_1$ adquire uma velocidade horizontal $v_1$ e cai a uma distância $x_0+l$ do ponto de lançamento,

Onde o tempo de queda da massa $m_1$ é dado pelo tempo de queda livre,

$$0=y_0-\frac{1}{2}gt_q^2\Rightarrow$$
$$t_q=\sqrt{\frac{2y_0}{g}}\ \ \ (5)$$

A distância em que o a massa mais pesada $m_1$ cai do ponto de lançamento é dada por,

$$x_f=x_0+v_1t_q$$

Explicitando $v_1$ obtemos,

$$v_1=\frac{x_f-x_0}{t_q}$$

Substituindo (5) e (4) na equação teremos,

$$v_1=\left( x_f-2y_0\cot\theta\right)\sqrt{\frac{g}{2y_0}}\ \ \ \ \ (6)$$

No inicio do movimento o momento total era,

$$P_i=\left( m_1+m_2\right)v_0\cos\theta\Rightarrow$$
$$P_i=\left( m_1+m_2\right)\sqrt{2gy_0}\cot\theta$$

O momento logo após a explosão é dado por,

$$P_f=m_1v_1+v_2m_2\Rightarrow$$
$$P_f=m_1\left( x_f-2y_0\cot\theta\right)\sqrt{\frac{g}{2y_0}}+v_2m_2$$

Supondo que o momento é conservado no processo obtemos,

$$P_i=P_f\Rightarrow$$
$$\left( m_1+m_2\right)\sqrt{2gy_0}\cot\theta=m_1\left( x_f-2y_0\cot\theta\right)\sqrt{\frac{g}{2y_0}}+v_2m_2$$

Explicitando $v_2$ obtemos,

$$v_2=\frac{\left( m_1+m_2\right)}{m_2}\sqrt{2gy_0}\cot\theta-\frac{m_1}{m_2}\left( x_f-2y_0\cot\theta\right)\sqrt{\frac{g}{2y_0}}\ \ \ \ (7)$$

A distância $x_m$ que o fragmento mais leve percorre é dado por,

$$x_m=v_2t_q\Rightarrow$$

Substituindo (7) e (5) obtemos,

$$x_m=\frac{\left( m_1+m_2\right)}{m_2}2y_0\cot\theta-\frac{m_1}{m_2}\left( x_f-2y_0\cot\theta\right)$$
Substituindo os valores,
$$\left\lbrace \begin{array}{llllll}
m_1=0,1m\\
m_2=0,05m\\
x_f=90m\\
g=9,8m/s^2\\
y_0=25m\\
\theta=45°\\
\end{array}\right. $$

$$x_m=120m$$
b) as velocidades na horizontal são dadas por (7), (6) e (1)

$$\left\lbrace \begin{array}{lll}
v_2=\frac{\left( m_1+m_2\right)}{m_2}\sqrt{2gy_0}\cot\theta-\frac{m_1}{m_2}\left( x_f-2y_0\cot\theta\right)\sqrt{\frac{g}{2y_0}}\\
v_1=\left( x_f-2y_0\cot\theta\right)\sqrt{\frac{g}{2y_0}}\\
v_{0x}=\frac{\sqrt{2gy_0}}{\sin\theta}\cos\theta\\
\end{array}\right. $$

Substituindo os valores,

$$\left\lbrace \begin{array}{llllll}
m_1=0,1m\\
m_2=0,05m\\
x_f=90m\\
g=9,8m/s^2\\
y_0=25m\\
\theta=45°\\
\end{array}\right. $$

Obtemos,

$$\left\lbrace \begin{array}{lll}
v_1=17,1m/s\\
v_2=30,9m/s\\
v_{0x}=22,1m/s\\
\end{array}\right. $$

As velocidades comunicadas a cada fragmento são dadas por,

$$\left\lbrace \begin{array}{ll}
v_{c1}=v_1-v_0=17,1m/s-22,1m/s=-4,42m/s\\
v_{c2}=v_2-v_0=30,9m/s-22,1m/s=8,85m/s\\
\end{array}\right. $$

c) Podemos calcular a variação da energia cinética do sistema e obter a energia fornecida pela explosão,

$$\Delta E_T=\frac{1}{2}(m_1+m_2)v_{0x}^2-\frac{1}{2}m_1v_1^2-\frac{1}{2}m_2v_2^2$$

Substituindo os valores obtemos,

$$\Delta E_T=2,8J$$