8.9) Uma mina explode em três fragmentos, de 100 g cada um, que se deslocam num plano horizontal: um deles para oeste e os outros dois em direções 60° ao norte e 30° ao sul da direção leste, respectivamente. A energia cinética total liberada pela explosão é de 4. 000 J. Ache as velocidades iniciais dos três fragmentos.
Olhando para a explosão do alto, podemos adotar o referencial com origem no centro da explosão,
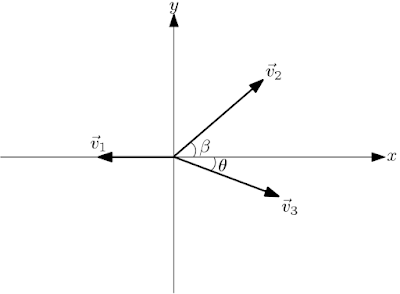
As velocidades comunicadas as massa pela explosão são $\vec{v}_1$, $\vec{v}_2$ e $\vec{v}_3$, respectivamente, uma delas segue na direção $ox$ negativo com velocidade $\vec{v}_1$ enquanto as outras duas são lançadas na direção leste $\theta$ sul com velocidade $\vec{v}_3$ e leste $\beta$ norte com velocidade $\vec{v}_2$, respectivamente. Antes da explosão o momento do sistema é nulo $\vec{P}_i=0$, por outro lado depois da explosão o momento do sistema será,
$$\vec{P}_f=m\vec{v}_1+m\vec{v}_2+m\vec{v}_3\ \ \ (1)$$
Decompondo os vetores sobre o referencial adotado obtemos,
$$\vec{P}_f=-mv_1\hat{i}+mv_2\cos\beta\hat{i}+mv_2\sin\beta\hat{j}+mv_3\cos\theta\hat{i}-mv_3\sin\theta\hat{j}\Rightarrow$$
$$\vec{P}_f=\left( mv_2\cos\beta-mv_1+mv_3\cos\theta\right) \hat{i}+\left(mv_2\sin\beta-mv_3\sin\theta\right) \hat{j}$$
Usando conservação de momento,
$$\vec{P}_i=\vec{P}_f\Rightarrow$$
$$0=\left(mv_2\cos\beta-mv_1+mv_3\cos\theta\right) \hat{i}-\left(mv_2\sin\beta-mv_3\sin\theta\right) \hat{j}\ \ \ (2)$$
Igualando componente a componente da equação obtemos as seguintes equações,
$$\left\lbrace \begin{array}{ll}
v_2\cos\beta-v_1+v_3\cos\theta=0\ \ \ (3)\\
v_2\sin\beta-v_3\sin\theta=0\ \ \ (4)\\
\end{array}\right. $$
Ao explodir a bomba comunica um total $E$ de energia aos três fragmentos, que se manifesta como energia cinética logo,
$$\frac{1}{2}mv_1^2+\frac{1}{2}mv_2^2+\frac{1}{2}mv_3^2=E\Rightarrow$$
$$v_1^2+v_2^2+v_3^2=\frac{2E}{m}\ \ \ \ (5)$$
Isolando $v_2$ na equação (4),
$$v_2=\frac{\sin\theta}{\sin\beta} v_3\ \ \ (6)$$
Aplicando o resultado (6) na equação (3),
$$v_1=\left(\sin\theta\cot\beta+\cos\theta\right) v_3\ \ \ (7)$$
Aplicando os resultados (7) em (5) encontramos,
$$\left(\sin\theta\cot\beta+\cos\theta\right)^2 v_3^2+\frac{\sin^2\theta}{\sin^2\beta} v_3^2+v_3^2=\frac{2E}{m}$$
Explicitando $v_3$,
$$v_3=\sqrt{\frac{2E}{m\left[ \left(\sin\theta\cot\beta+\cos\theta\right)^2+\frac{\sin^2\theta}{\sin^2\beta}+1\right]}}\ \ \ (8)$$
Aplicando (8) em (6) e (7) teremos as seguintes soluções,
$$\left\lbrace\begin{array}{lll}
v_1=\left(\sin\theta\cot\beta+\cos\theta\right)\sqrt{\frac{2E}{m\left[ \left(\sin\theta\cot\beta+\cos\theta\right)^2+\frac{\sin^2\theta}{\sin^2\beta}+1\right]}}\\
v_2=\frac{\sin\theta}{\sin\beta}\sqrt{\frac{2E}{m\left[ \left(\sin\theta\cot\beta+\cos\theta\right)^2+\frac{\sin^2\theta}{\sin^2\beta}+1\right]}}\\
v_3=\sqrt{\frac{2E}{m\left[ \left(\sin\theta\cot\beta+\cos\theta\right)^2+\frac{\sin^2\theta}{\sin^2\beta}+1\right]}}\\
\end{array}\right. $$
Os valores associados ao problema são,
$$\left\lbrace \begin{array}{ll}
m=0,1kg\\
E=4000J\\
\theta=30°\\
\beta=60°\\
\end{array}\right. $$
Substituindo os valores encontramos,
$$\left\lbrace \begin{array}{lll}
v_3=173,2m/s\\
v_2=100m/s\\
v_1=200m/s\\
\end{array}\right. $$
Comentários