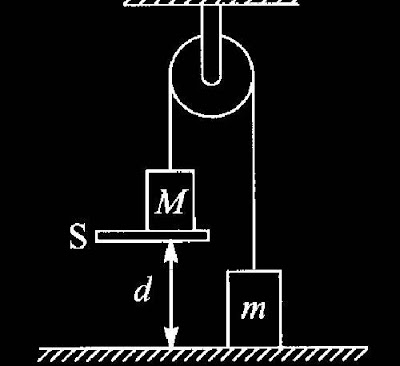
6.2) No sistema da figura, $M=3kg$, $m=1kg$ e $d=2m$. O suporte $S$ é retirado num dado instante. (a) Usando conservação de energia, ache com que velocidade $M$ chega ao chão. (b) Verifique o resultado, calculando a aceleração do sistema pelas leis de Newton.
Adotando o referencial de $M$ no nível do solo $S$ e de $m$ no nível da plataforma, podemos representar as informações do sistema com mais clareza,

Se a energia associada ao sistema é constante então, supondo que a massa da polia seja desprezível assim como a massa das cordas, teremos que a variação da energia é nula,
$$\Delta E=0\Rightarrow$$
$$E_i=E_f\ \ \ (1)$$
No primeiro instante o aparato tem apenas uma energia potencial gravitacional associada ao sistema, que é dada pelos seus respectivos referenciais inerciais,
$$E_i=Mgh-mgh\ \ \ (2)$$
No segundo momento a energia potencial é totalmente convertido em energia cinética, ou seja,
$$E_f=\frac{1}{2}Mv^2+\frac{1}{2}mv^2\ \ \ (3)$$
Usando a equação (2) e (3) em (1) obtemos a seguinte relação,
$$Mgh-mgh=\frac{1}{2}Mv^2+\frac{1}{2}mv^2$$
Explicitando a velocidade obtemos,
$$v=-\sqrt{2gh\frac{M-m}{M+m}}$$
Por outro lado, podemos usar as leis de Newton para chegar a mesma conclusão, adotando os referenciais sobre os blocos de massa $M$ e $m$ podemos representar as forças que atuam sobre o sistema durante o movimento,

Usando a segunda lei de Newton obtemos as equações que descrevem o movimento,
$$\left\lbrace \begin{array}{ll}
T-P_M=-Ma\ \ (4)\\
T-P_m=ma\ \ (5)\\
\end{array}\right. $$
Subtraindo (4) por (5) obtemos,
$$P_M-P_m=Ma-ma$$
Explicitando $a$ obtemos,
$$a=\frac{(M-m)g}{(M+m)}$$
O sistema descreve um movimento uniformemente acelerado adotando o referencial no solo o movimento é descrito por,
$$y=d-\frac{1}{2}\frac{(M-m)g}{(M+m)}t^2\ \ \ (6)$$
No momento em que o bloco de massa $M$ toca o solo $y=0$, dessa forma podemos calcular o tempo $t_q$ de queda,
$$0=d-\frac{1}{2}\frac{(M-m)g}{(M+m)}t_q^2\Rightarrow$$
$$\frac{1}{2}\frac{(M-m)g}{(M+m)}t_q^2=d\Rightarrow$$
$$t_q^2=2d\frac{(M+m)}{(M-m)g}\Rightarrow$$
$$t_q=\sqrt{2d\frac{(M+m)}{(M-m)g}}\ \ \ (7)$$
Derivando (6) em função do tempo obtemos a velocidade $v$,
$$v=-\frac{(M-m)g}{(M+m)}t\ \ \ (8)$$
Substituindo (7) em (8) obtemos a velocidade de queda,
$$v=-\frac{(M-m)g}{(M+m)}\sqrt{2d\frac{(M+m)}{(M-m)g}}\Rightarrow$$
$$v=-\sqrt{2d\frac{(M-m)^2g^2(M+m)}{(M+m)^2(M-m)g}}\Rightarrow$$
$$v=-\sqrt{2dg\frac{M-m}{M+m}}$$
Substituindo os valores do problema obtemos,
$$v=-4,42m/s$$




Comentários